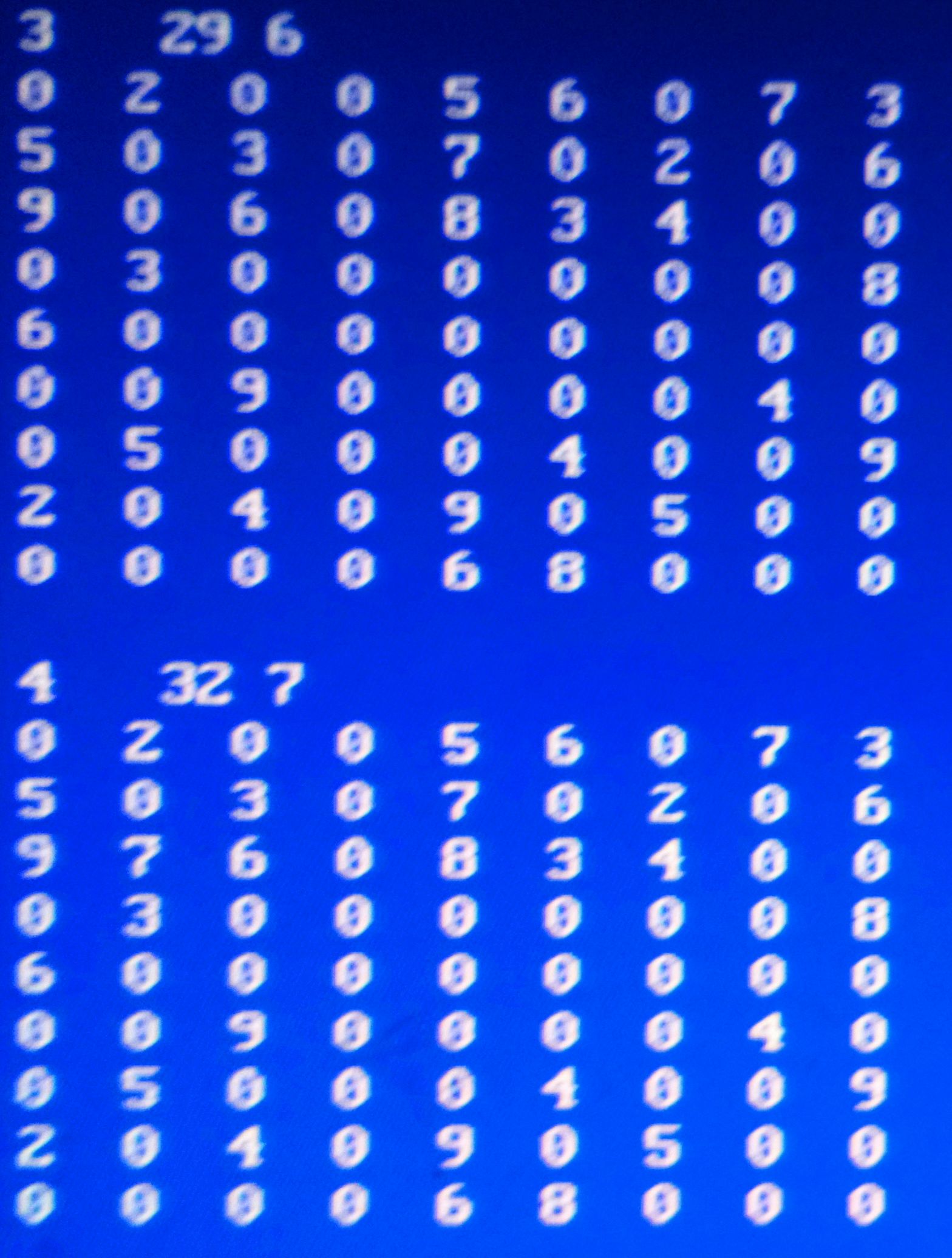
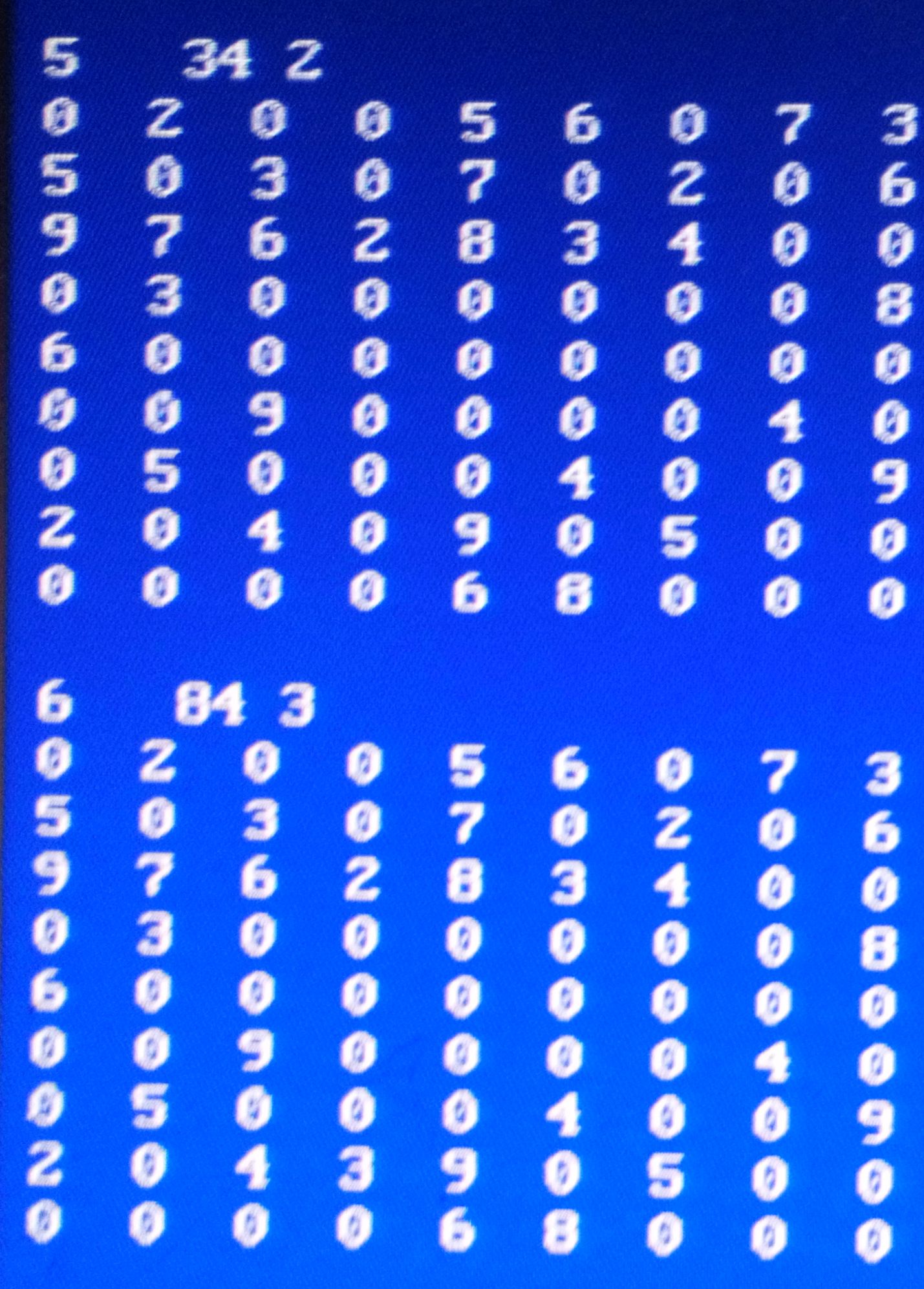
Sudoku for dummies.

Enklaste sättet att lösa en sudoku är när man ser vilka siffror som ska skrivas in i de tomma rutorna och sen gör det. För dem som inte har denna medfödda begåvning återstår ett mera systematiskt sökande på en liten del av spelplanen i taget. Spelplanens 81 rutor har 9 rader, 9 kolumner och 9 block som alla ska ifyllas med siffrorna 1 till 9. Ingen siffra får upprepas i någon rad, kolumn eller block. Knepigt värre.

Ett sätt att lösa är att börja i något block och se om siffran 1 kan fyllas i. Finns den redan går man till siffran 2 för att på sikt beta av alla fram till 9. Om ingen siffra 2 ännu finns i blocket kollar man i de rader och kolumner som går genom blocket om det finns någon 2:a på dem. Finns det en så kan man inte fylla in en 2:a på rutorna som den raden/kolumnen har i blocket.

Har man gått igenom alla nio siffrorna i ett block går man till nästa och så vidare genom hela spelplanen. Tidsödande, metodiskt och enda belöningen är att man kanske till slut har fyllt i alla rutorna.

När man nu ändå koncentrerar sig på en mindre del av spelplanen i taget kan man titta närmare på de delvis ifylla raderna. Om raden har bara en tom ruta fyller man bara i den saknade siffran. Är det två rutor som är tomma kollar man på kolumnerna som går igenom dem. Om din rad saknar en 2:a och den ena kolumnen har en 2:a och den andra inte så är man säker på att där kan man fylla i en 2:a och sedan fyller man i den återstående tomma rutan. Är det fler tomma rutor på raden så gäller att de tomma rutor som finns i samma block inte kan ha de siffror som redan finns i just det blocket, däremot kan de ju platsa på en annan del av raden. Det som sagts om rader gäller förstås också om kolumner.

Sedan kan man kolla över hela spelplanen, siffra för siffra. Har två block en 2:a så kanske man kan se var det tredje blocket ska ha en 2:a. Genom att koncentrare sig på en aspekt i taget ser man ofta lösningar som förut missats.

Möter en rad en kolumn i ett blocks tomma ruta kan man kolla vilka 8 siffror som finns ifyllda, då platsar den 9:e i den tomma rutan.

De ovan presenterade teknikerna används iterativt och ser man en ruta man kan fylla i så gör man det, spelplanen ändras rätt mycket varje gång en ruta fylls i. Till slut efter ett antal omgångar är man färdig för ett nytt sudoku.

Ska man klara av sudoku som är mera avancerat än lätt- och medelsvår behöver man föra logiska resonemang. Enklare sådana blir det ju även vid ovanstående metoder, men vid en svår sudoku vet jag inte hur man bryter ner den i enklare delar. En början ger följande exempel. Av tre block i rad har ett en rad där det finns en 2:a. Block två har en annan rad med en tom ruta. Tredje blocket har denna rad helt ifylld men två eller tre tomma kolumner på en tredje rad. Någonstans på denna rad ska det komma en 2:a, okänt var. Dock är det nu känt på vilken rad 2:an i block 2 ska placeras, och där hade vi en tom ruta som kan fyllas i. Med mer övning kan man komplettera ovanstående tekniker med mer avancerade tillvägagångssätt.

Eftersom det är fler som beskrivit tillvägagångssättet finns det också bra illustrationer och bilder på nätet-

Det finns andra tekniker för att lösa en sudoku, en generell teknik visas här

Det finns program för att konstruera en sudoku och program för att lösa dem. Genom att testa alla möjligheter är alla sudokus möjliga att lösa. Att visa steg för steg hur man ska göra går också. Gör man programmet för avancerat kan det bli svårt att förstå varför datorn gör ett visst drag och då har ju finessen med att visa stegvis förrsvunnit. Därtill kommer alltid problemet att de metoder man programmerar in inte är tillräckliga för alla sudokus och då måste man lista ut nya vägar för lösandet med nya program som följd.

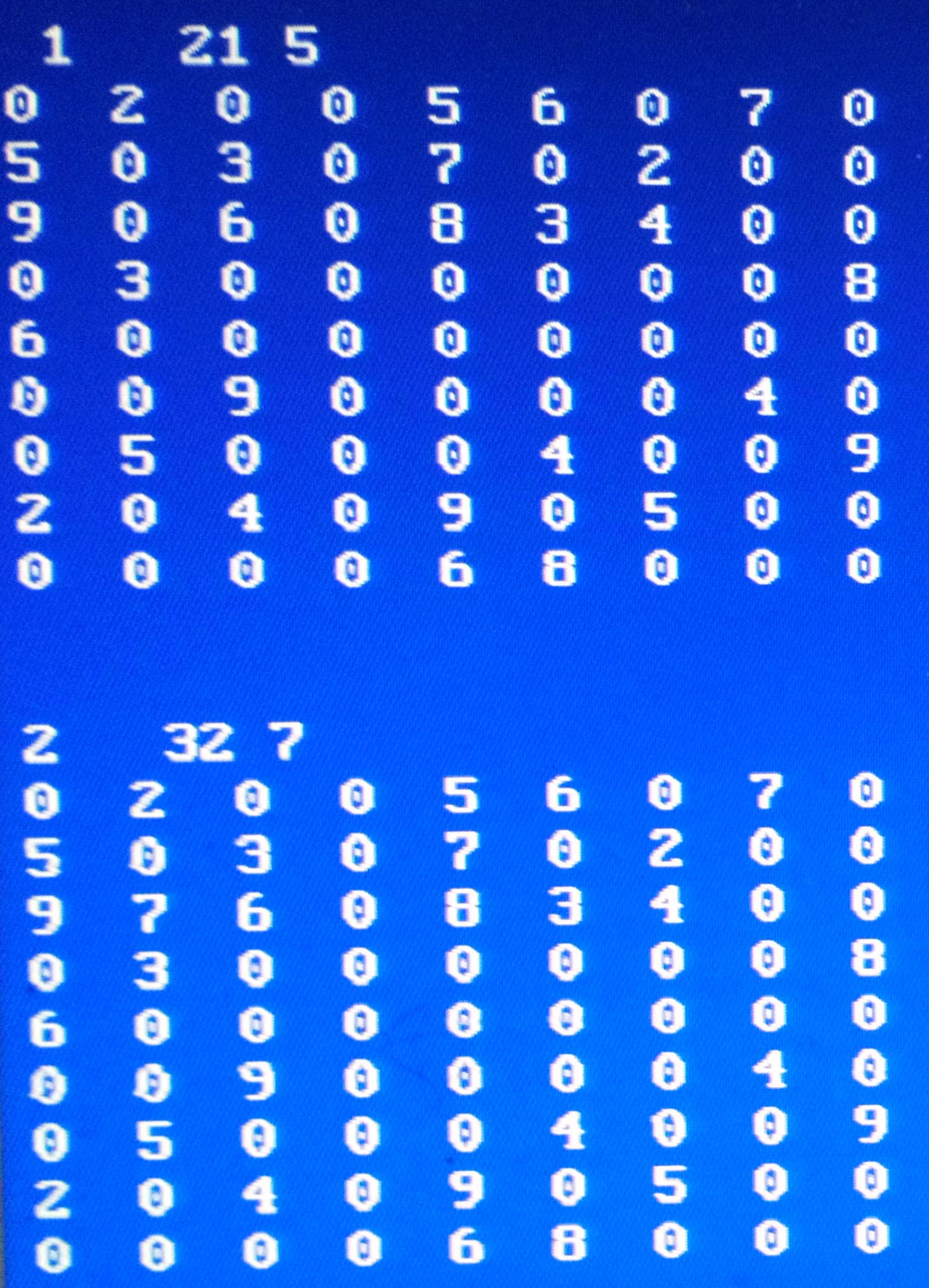
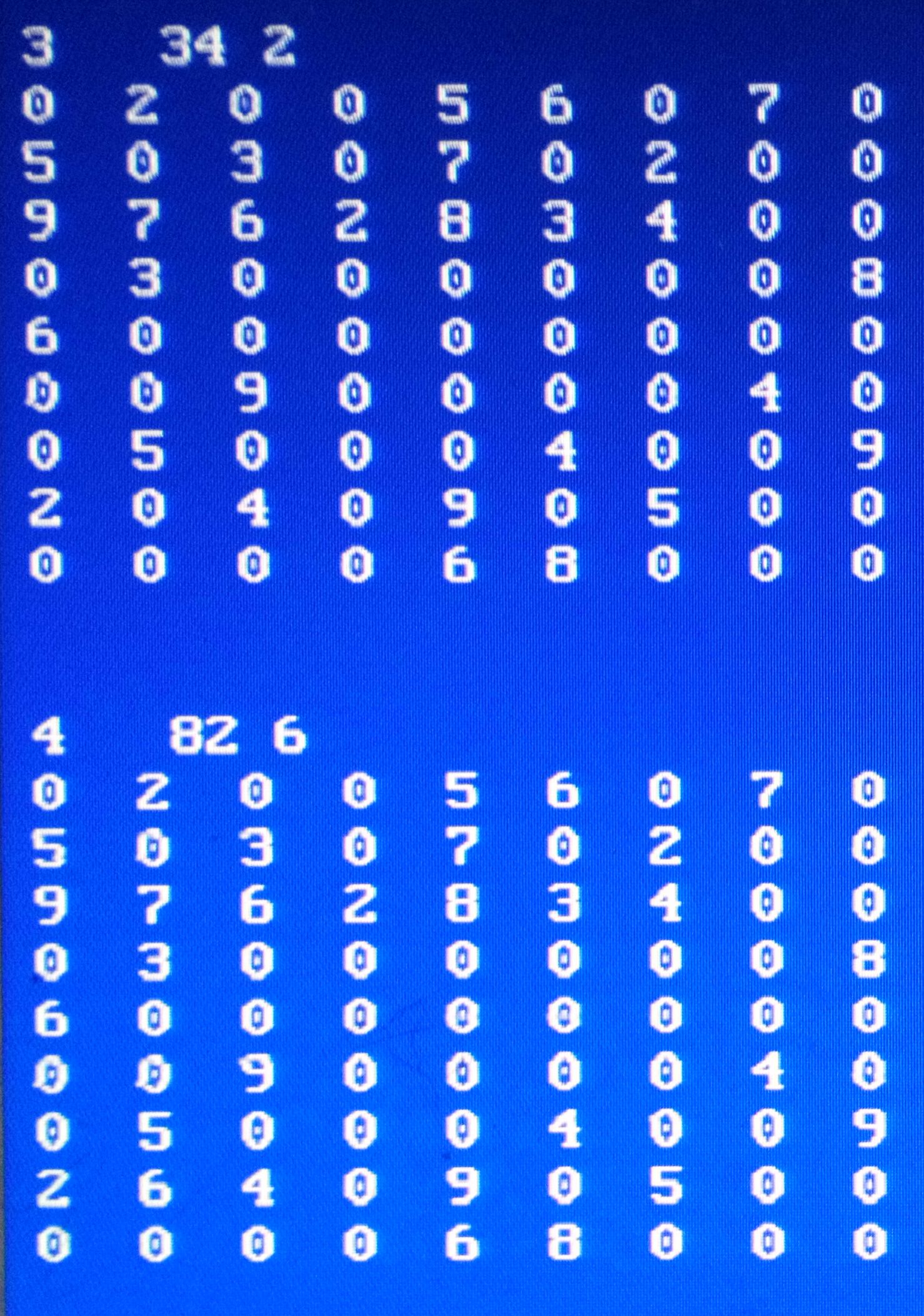
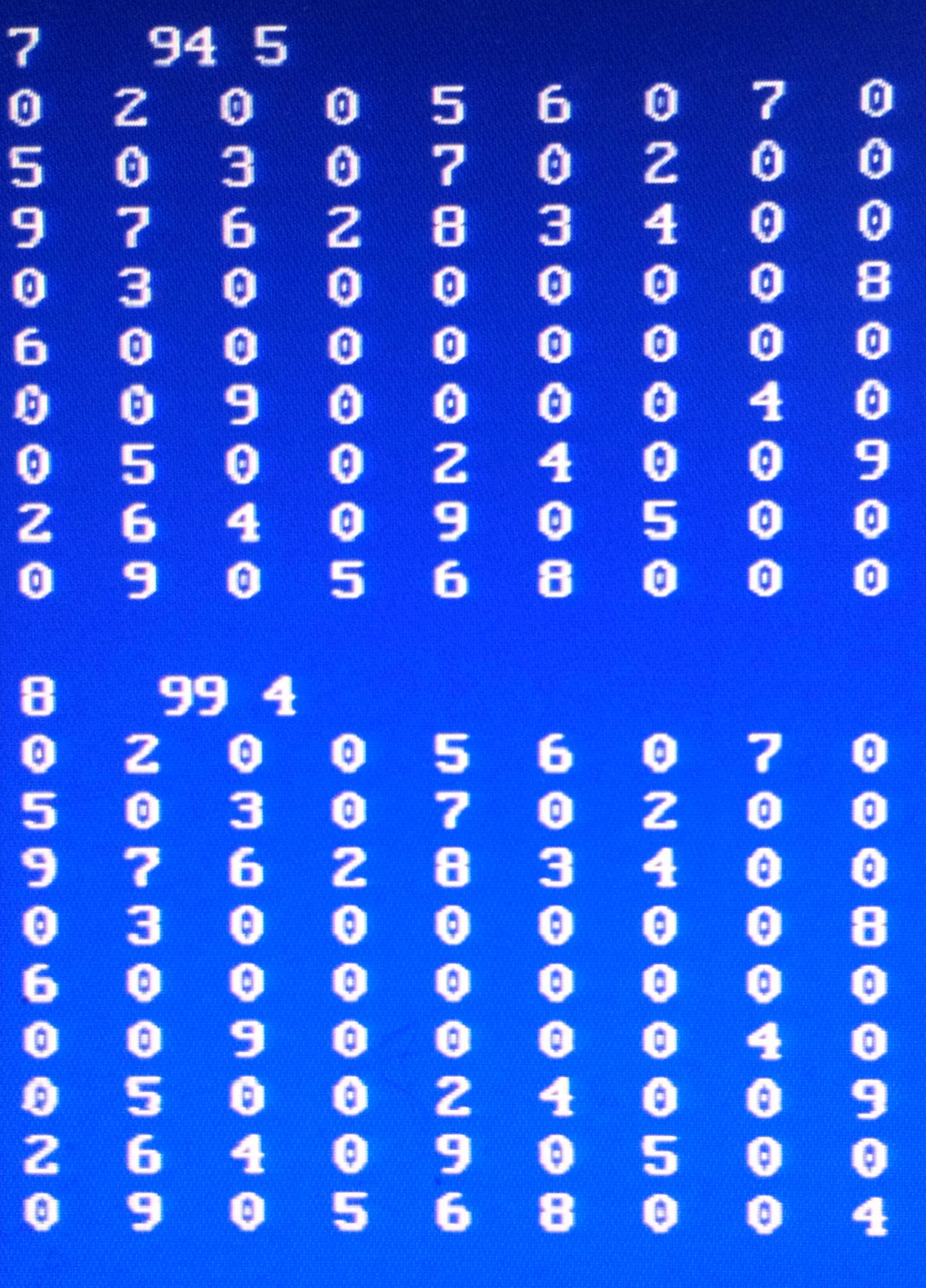
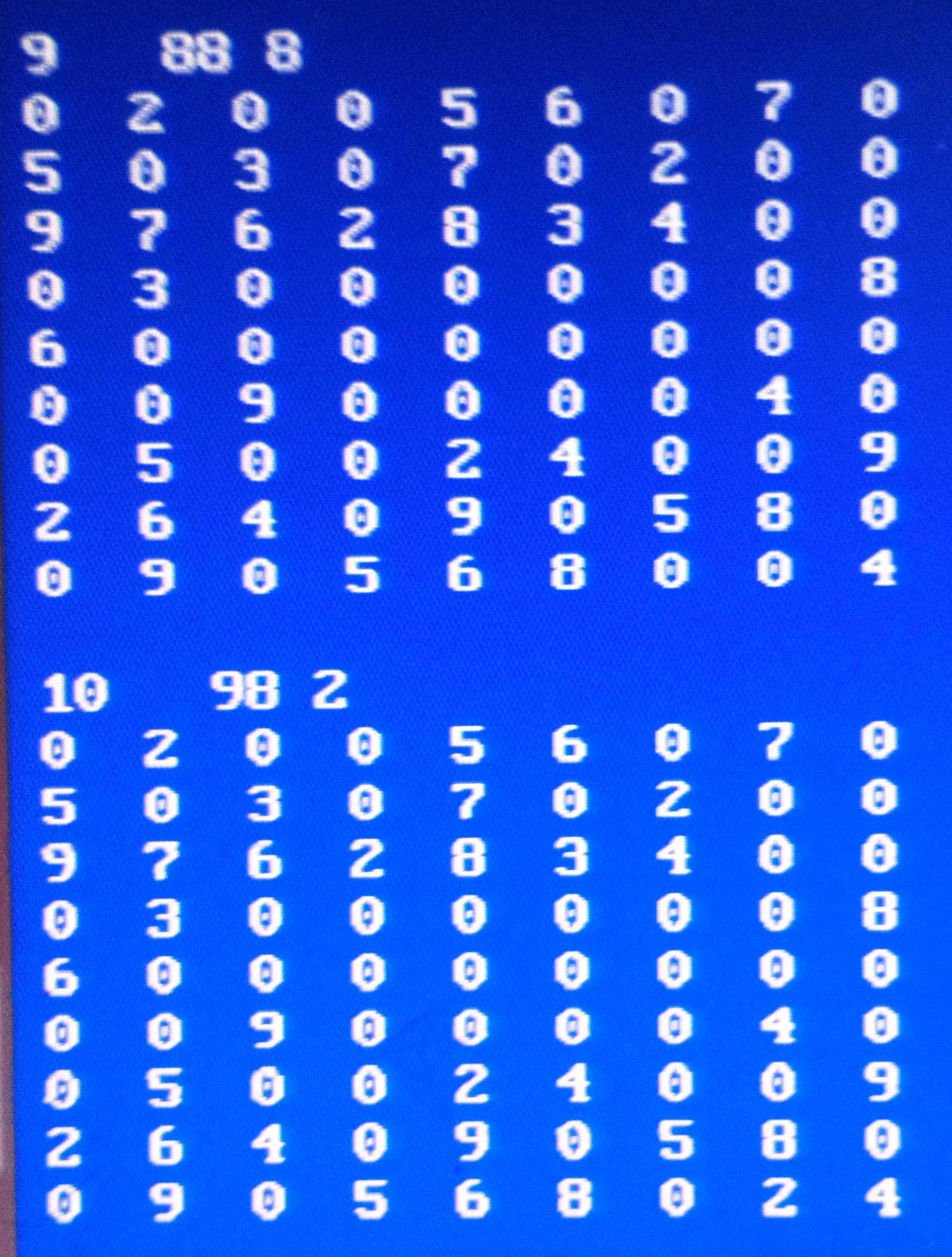
Nedan först en sudoku och sedan två rader med lösningar, steg för steg. Den första visar en enkel där rader och kolumner styr vad man kan fylla i. Den nedre raden visar en videreutveckling i programmet, logisk men svår för en människa att förstå de enskilda dragen. Rätt blir det och den ena kan lösa en sudoku som den andre går bet på. Men man vet inte altid riktigt hur det gick till.

Jozef Saers