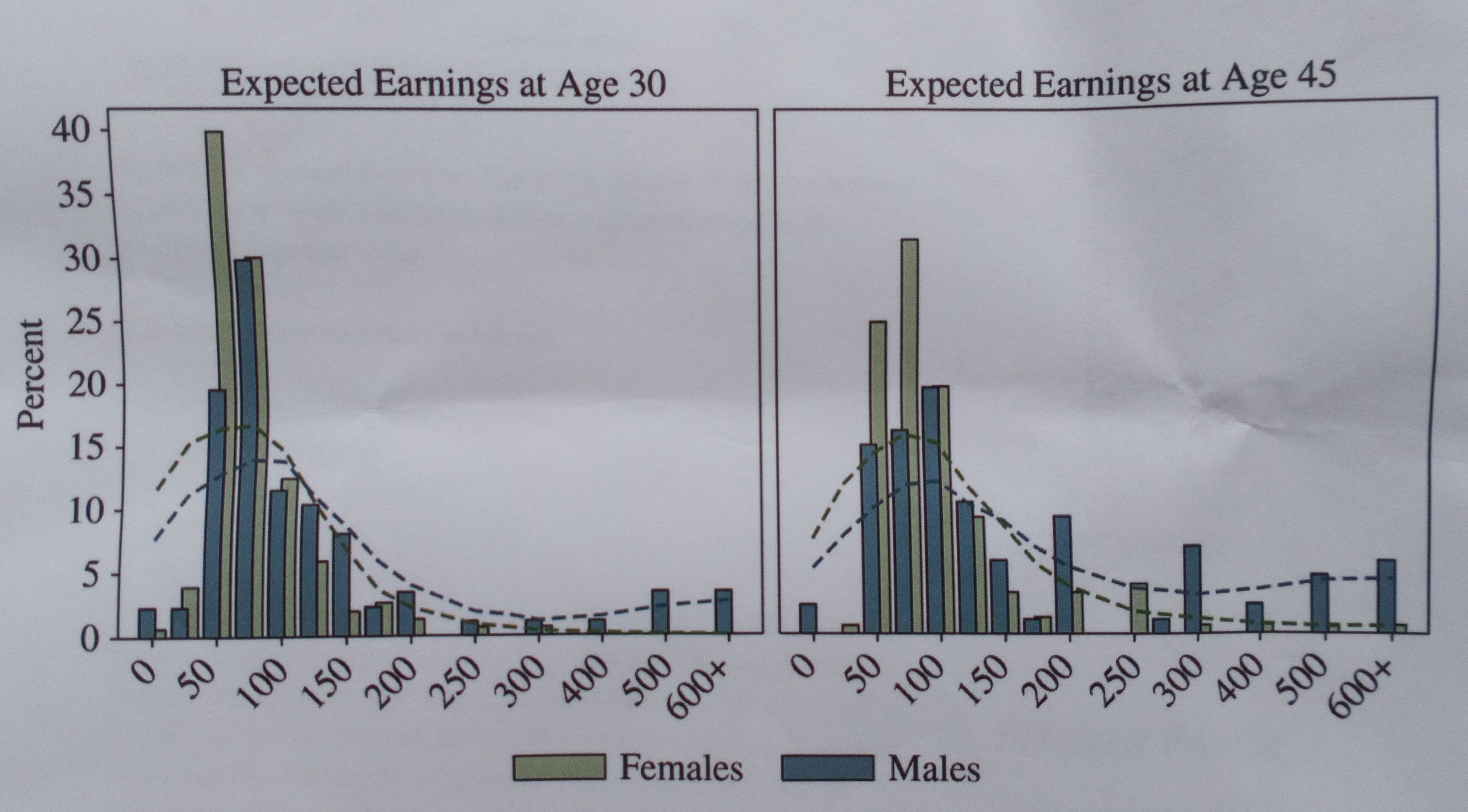
På nätet hittades nedanstående bild över inkomster, en skev fördelning med spridda förekomster vid höga värden. Hade skalan logaritmerats hade fördelningen säkert mera liknat en normalfördelning med några avvikare.

När man gick i realskolan märkte man att det fanns en liten grupp mycket duktiga kamrater som alltid had Ab och a medan de fick nöja sig med B. Däremellan fanns nångon enstaka med Ba. Det kan läsas in i nedanstående samling amerikanska iq-värdena.

Hittade på nätet iq-värden för 300 pojkar och flickor på en tänkt Mayfield High school . De var uppdelde på högerhända flickor samt höger- resp vänsterhända pojkar. I den fjärde kolumnen anges en summering. Fördelningen verkar bestå av flera toppar, alla skevt fördelade och markerade med pilar.

Ett annat exempel är nedanstående med data från enäggstvillingar från olika undersökningar 1937 till 1966 ( Jensen 1970, table1). Även här förekommer toppar på samma ställen 99, 109, 116. Samtidigt visar olikheter i fördelningarna att testerna blivit olika utformade under årens lopp. För att fungera på flera platser och tidpunkter måste frågorna göras så att svaren blir normalfördelade, man kallibrerar alltså mätmetoderna så att utfallet blir en normalfördelning och man får en normalfördelning som resultat.

Man kan nu skapa en teori om att fördelningen är en effekt av rekombinationer av gener. Förekomsten av toppar vid sidan av huvudgruppen kan då ses som en tillgång i svåra lägen, som nödår och katsstroflägen där bara ett fåtal överlever, men där det dock finns sådana som klarar ytterligheter.

Om den genetiska bakgrunden till IQ i multipla alleller se tex Weiss 1991. De mindre topparna vid sidan om normalfördelningen kan förklaras med en summering av flera normalfördelningar av olika storlek på lite olika ställen på skalan.

Litt:

AR Jensen Iq's of identical twins reared apart, Behaviour Genetics, Voll, No.2, 133-146.

V Weiss Major genes of general inelligence. In: Personality and individual Differences 13, 1992.

Jozef Saers